CURVA ROC: INTRODUCCIÓN

ÍNDICE

¡Bienvenidx!, soy Interneuronamed y te explicaré un poco sobre las curvas ROC. Este tema está dividido en tres apartados, aquí te mostraré algunas generalidades y conceptos básicos. En los siguientes dos artículos te hablaré acerca de su interpretación y un ejemplo/ejercicio de análisis.

No olvides seguirme en mis redes sociales como Interneuronamed, y en el botón azul de Google+ que se encuentran en la parte inferior de este artículo. 

INTRODUCCIÓN A LA CURVA ROC

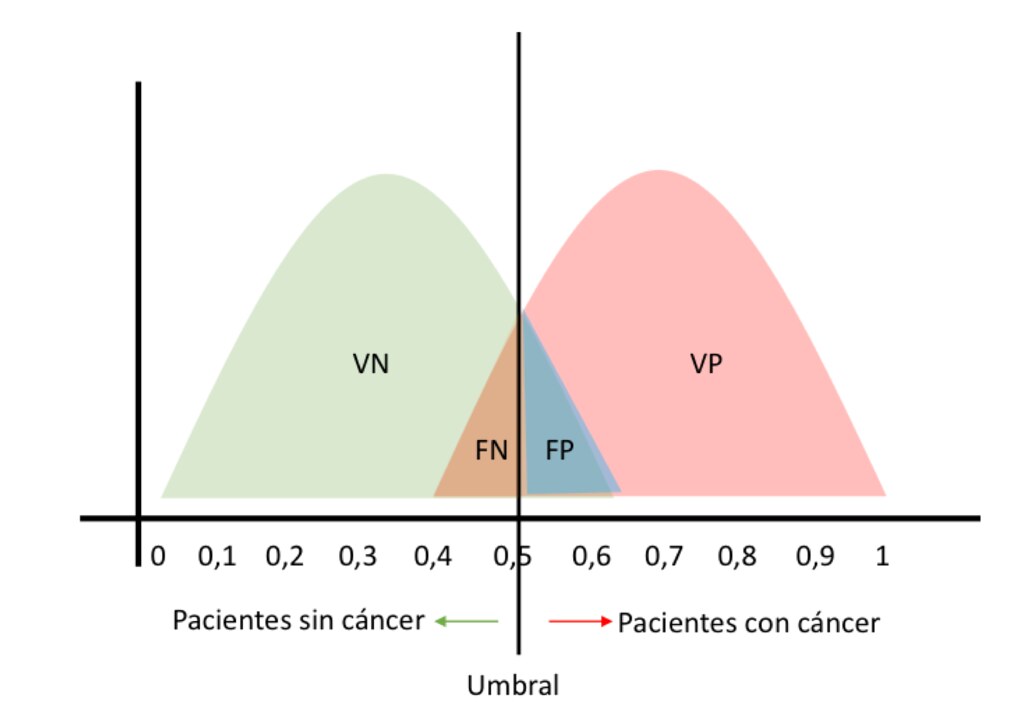
Las curvas ROC son utilizadas para la representación gráfica de la relación entre la sensibilidad y la especificidad para cada posible punto de corte de una prueba diagnóstica o para una combinación de pruebas. También es importante que sepas que el término ROC significa Característica de Funcionamiento del Receptor. En otras palabras, la curva ROC, cuantifica la capacidad de una prueba diagnóstica para discriminar entre sanos y enfermos.

No es nada fácil tomar una decisión clínica donde debemos conocer perfectamente la eficacia y exactitud de las pruebas diagnósticas, es decir, su capacidad para clasificar correctamente a los pacientes. Habitualmente, la clasificación es dicotómica (en dos categorías): paciente enfermo o paciente no enfermo.

Sin embargo, nos estamos limitando al enfoque de eficacia diagnóstica (sensibilidad y especificidad diagnóstica), dejando a un lado pruebas diagnósticas que se miden utilizando escalas ya sean continuas o discretas ordinales. Por ejemplo, en la evaluación de función renal a través de la eficacia de la creatinina, la evaluación de la función hepática a través de la eficacia de la bilirrubina y transaminasas, o en la evaluación inmunohistoquímica donde los resultados son presentados en porcentajes de presencia de reacción.

Tomando en cuenta que ya no estamos analizando una respuesta dicotómica, sino un conjunto de respuestas dicotómicas correspondientes a un nivel de decisión distinto, debemos elegir puntos de corte que puedan permitir una clasificación dicotómica a partir de un resultado que puede ser superior o inferior al punto de corte. Entonces, al representar gráficamente las respuestas dicotómicas obtenidas considerando todos los posibles puntos de corte de la o las pruebas diagnósticas, la curva ROC nos aportará una visión general de la eficacia y exactitud de la prueba diagnóstica. 

USOS Y LIMITACIONES DE LA CURVA ROC

Ahora bien, a continuación, encontrarás una lista de los usos clínicos y estadísticos de la curva ROC:

• Útiles para conocer el rendimiento general de una prueba diagnóstica a partir del análisis del área bajo la curva (ABC).
• Comparar dos pruebas diagnósticas.
• Comparar dos puntos de corte de una misma prueba diagnóstica.
• Comparar dos curvas o dos puntos sobre una curva.
• Para elegir el punto de corte apropiado para un determinado paciente.
• Representación gráfica de la relación entre sensibilidad y especificidad para cada posible punto de corte de una prueba o combinación de pruebas.
• El área bajo la curva ROC nos permite tener una visión global del beneficio de utilizar las pruebas diagnósticas en estudio.
• Útil para predecir la probabilidad de una respuesta dicotómica.
• Son útiles para evaluar modelos predictivos u otras pruebas que producen valores de salida en un rango continuo, ya que captura la compensación entre sensibilidad y especificidad en ese rango.
• 
  

Aunque pueda tener un listado largo de utilidad, también tiene sus limitaciones dentro de las pruebas que sólo contemplan respuestas dicotómicas. No permite su aplicación en situaciones donde tenemos que distinguir entre más de dos enfermedades o eventos de interés.

ÁREA BAJO LA CURVA ROC

Otro punto introductorio importante es el área bajo la curva (ABC) ROC. Una Curva ROC se puede construir a partir de métodos no paramétricos (ej. Empírico), que no suponen una distribución normal de los resultados de la prueba diagnóstica, o métodos paramétricos (ej. Binormal) que suponen una distribución determinada para la variable de decisión.

La curva ROC como herramienta útil para predecir la probabilidad de una respuesta dicotómica, es un gráfico de la tasa de falsos positivos en las abscisas (eje X) versus la tasa de verdaderos positivos en las ordenadas (eje Y) para un conjunto de valores de umbral candidatos distintos entre 0 y 1, es decir que los ejes del gráfico adoptan valores entre 0 y 1 que representan del 0% al 100%, delimitando un cuadrado de área igual a 1. Entonces, una prueba diagnóstica se va a considerar no-discriminativo, es decir que no permite diferenciar entre sanos y enfermos, si su curva ROC coincide con la línea de no-discriminación que tiene un área bajo la curva igual a 0.5. Lo anterior se traduce a una diagonal que divide en dos mitades iguales el cuadrado de área que era igual a 1. A medida que el ABC-Roc de una prueba diagnóstica se acerca al 1 (hacia arriba y hacia la izquierda), mayor será su capacidad discriminativa.  En otras palabras, sanos vs enfermos, donde los valores más pequeños en el eje X del gráfico indican menos falsos positivos y menores falsos negativos.

El área bajo la curva ROC se puede emplear como un índice a conveniencia de la eficacia global de una prueba diagnóstica: la exactitud máxima correspondería a un valor del Área Bajo la Curva de 1 y la mínima a uno de 0.5. En el caso de que fuere un valor <0.5, debería invertirse el criterio de positividad de la prueba.

Por último y como pequeño antecedente al próximo artículo de análisis de una curva ROC, hay consideraciones que debes tomar en cuenta para seleccionar el punto de corte. Entre las consideraciones está el tomar en cuenta los riesgos y beneficios de las decisiones médicas a partir del resultado de la prueba diagnóstica. El uso de una prueba diagnóstica nos exige elegir un valor de corte.

El mejor punto de corte para elegir tiene una tasa de verdaderos positivos más alta combinada con una tasa de falsos positivos más baja. Debido a que el área bajo la curva ROC es una medida de la utilidad de una prueba diagnóstica, donde un área mayor representa la mayor utilidad, las áreas bajo la curva ROC son utilizadas para hacer una comparación de la utilidad de las pruebas diagnósticas.

REFERENCIAS BIBLIOGRÁFICAS

Cerda Jaime, Cifuentes Lorena. Uso de curvas ROC en investigación clínica: Aspectos teórico-prácticos. Rev. chil. infectol.  [Internet]. 2012  Abr [citado  2020  Dic  23] ;  29( 2 ): 138-141. Disponible en: https://scielo.conicyt.cl/scielo.php?script=sci_arttext&pid=S0716-10182012000200003&lng=es.  http://dx.doi.org/10.4067/S0716-10182012000200003.

López de Ullibarri Galparsoro I, Píta Fernández, S. Curvas ROC. España: Fisterra; 2001 Sep [Revisado 2020 Dic 23]. Disponible en: https://www.fisterra.com/mbe/investiga/curvas_roc/curvas_roc.asp#Figura%202 

¿CÓMO CITAR ESTE ARTÍCULO?

Medina I. Curva ROC: INTRODUCCIÓN [Internet]. México: Interneuronamed; 2020 dic. [revisado; consultado]. Disponible en: https://interneuronamed.blogspot.com/2021/01/curva-ROC.html

Únicamente editarás la sección de “[revisado; consultado]” con la fecha de hoy y con alguno de los siguientes formatos.

1. [revisado 20 dec 2021]
2. [consultado 20 dec 2021]